Nesta webaula, você compreenderá o conceito de tabela verdade.
Tanto o hardware como software computacional são baseados na lógica computacional, que, por sua vez, é baseada na lógica formal. Tudo é possível porque a lógica computacional produz somente resultados binários para suas fórmulas,
ou seja, Verdadeiro ou Falso.
As fórmulas podem ora ser valoradas em 0, em cujo caso a valoração falsifica a fórmula, ora ser valoradas em 1, em cujo caso a valoração satisfaz a fórmula. Estes fatos motivam a classificação das fórmulas de acordo com o seu comportamento diante de todas as valorações possíveis de seus átomos. Um dos grandes desafios da computação é encontrar métodos eficientes para decidir se uma fórmula é satisfazível/insatisfazível, ou se é válida/falsificável. Um dos primeiros métodos propostos na literatura para a verificação da satisfatibilidade e validade de fórmulas é o método da Tabela da Verdade.
A Tabela Verdade é um mecanismo que permite valorar fórmulas de forma genérica a partir de entradas binárias e conectores lógicos.
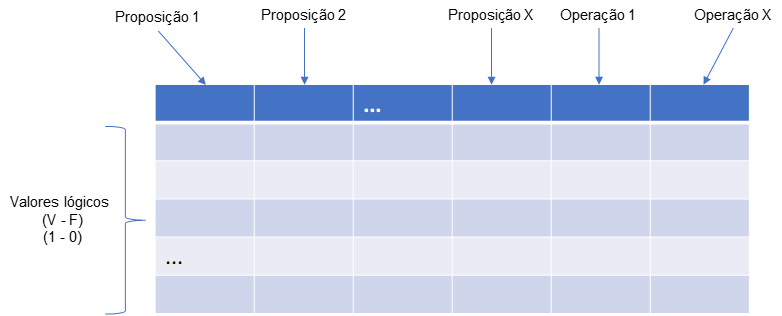
A Figura 1 mostra o esquema geral para uma Tabela Verdade. Nas primeiras colunas coloca-se as proposições (quantas forem necessárias testar), em seguida, coloca-se as operações lógicas que se deseja valorar. Nas linhas são colocadas
os valores lógicos (V – F) tanto para as proposições quanto para os resultados das fórmulas.
A quantidade de linhas (combinações) aumenta exponencialmente com a quantidade de proposições seguindo a regra , em que n é o número de proposições. Portanto, para duas
proposições tem-se linhas; para três proposições tem-se linhas; para quatro proposições tem-se linhas; e assim por diante.
O conectivo lógico de conjunção (AND - E) é utilizado para realizar uma operação binária entre duas proposições quando se deseja obter um resultado verdadeiro se, e somente se, as duas proposições forem verdadeiras. Confira a Figura
2 a seguir:

O conectivo lógico de disjunção (OR - OU) é utilizado para realizar uma operação binária entre duas proposições quando se deseja obter um resultado falso se, e somente se, as duas proposições forem falsas. Confira a Figura 3 a
seguir:

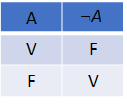
O operador lógico de negação tem a função de inverter seja uma entrada ou o resultado de uma operação. Confira a Figura 4 a seguir:
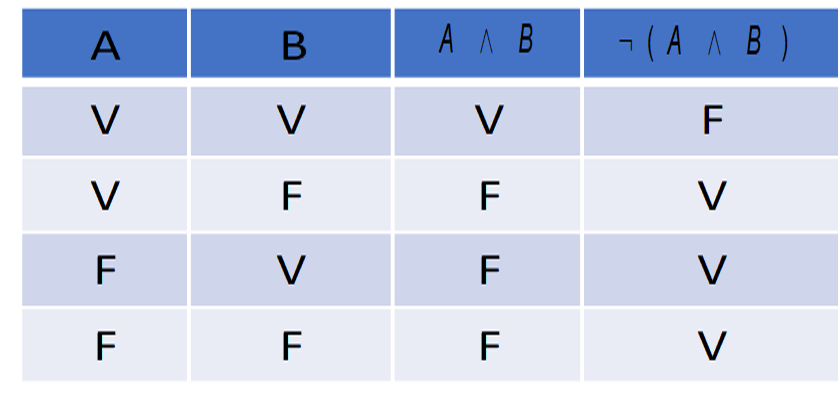
A Figura 5 mostra a negação do resultado de uma fórmula que possui a conjunção. Os parênteses na fórmula devem ser usados com consciência, pois influenciam o resultado. Na Figura 5, os parênteses indicam que a negação fora deles
deve inverter o resultado de tudo o que está dentro.
Para aprimorar seu conhecimento, recomendamos a leitura das 5 primeiras páginas da seguinte obra:
GERSTING, J. L. Fundamentos matemáticos para a ciência da computação: matemática discreta e suas aplicações. 7. ed. Rio de Janeiro: LTC, 2017. (Disponível na Biblioteca Virtual.)
Também recomendamos a leitura da página 9 a 15 da obra:
SILVA, F. S. C. da; FINGER, M.; MELO, A. C. V. de. Lógica para computação. 2. ed. São Paulo: Cengage Learning, 2017. (Também disponível na Biblioteca Virtual.)